Binary Bomb

Table of Contents
Introduction
This post is about my experience solving the Binary Bomb lab from the course Architecture 1001: x86-64 Assembly.
I solved it 2 times. One time using gdb (with symbols) on Remnux and one using WinDbg (without symbols) on Windows 10.
This post will describe my solution using WinDbg without symbols.
Universal Functions
Now, before going through phase_1() function, it is worth mentioning a couple of the functions that will be executed repeatedly before, after, and inside phase_*() functions.
Here they are:
00007FF6`88F611E0 (bomb+0x111e0)-printf()00007FF6`88F611D1 (bomb+0x111d1)-read_line()00007FF7`8B8C12C6 (bomb+0x112c6)-sscanf(). It is used in functionsphase_3tophase_5, which require 2 numbers as an input.00007FF7`8B8C10D2 (bomb+0x110d2)-read_six_numbers(). Function that parses our input into 6 pointers. It is used in functionsphase_2andphase_6, which require 6 numbers as an input.00007FF6`88F612A8 (bomb+0x112a8)-phase_defused()00007FF7`8B8C13B6 (bomb+0x113b6)-explode_bomb()
It also is important to describe functions read_line():
read_line (input) {
num_input_strings++
return fgets(input)
}strings_not_equal():
strings_not_equal (string_1, string_2) {
if ((length(string_1) != length(string_2)) or (string_1 != string_2))
return 1
else
return 0
}And read_six_numbers():
read_six_numbers (six_numbers, string) {
count_of_numbers = sscanf(string, "%d %d %d %d %d %d", six_numbers[0], six_numbers[1], six_numbers[2], six_numbers[3], six_numbers[4], six_numbers[5])
if (count_of_numbers != 6)
explode_bomb()
return count_of_numbers;
}Bomb Lab Execution Flow
The overall execution flow is like this:
num_input_strings = 0
FILE * our_input
if (length(argv) = 1)
our_input = fopen(stdin, "r")
if (length(argv) = 2)
our_input = fopen(argv[1], "r")
}
puts("Welcome to my fiendish little bomb. You have 6 phases with\nwhich to blow yourself up. Have a nice day!")
our_string_1 = read_line(our_input) // num_input_strings = 1
phase_1(our_string_1)
phase_defused()
puts("Phase 1 defused. How about the next one?")
our_string_2 = read_line(our_input) // num_input_strings = 2
phase_2(our_string_2)
phase_defused()
puts("That's number 2. Keep going!")
our_string_3 = read_line(our_input) // num_input_strings = 3
phase_3(our_string_3)
phase_defused()
puts("Halfway there!")
our_string_4 = read_line(our_input) // num_input_strings = 4
phase_4(our_string_4)
phase_defused()
puts("So you got that one. Try this one.")
our_string_5 = read_line(our_input) // num_input_strings = 5
phase_5(our_string_5)
phase_defused()
puts("Good work! On to the next...")
our_string_6 = read_line(our_input) // num_input_strings = 6
phase_6(our_string_6)
phase_defused()
fclose(our_input)You can ask me "What about the last message that phase_6() and the bomb overall were defused?". You see, this message is actually printed by bomb_defused() function if phase_6() function was successfully executed. More on this in the last section of the post!
Phase 1
The jump to the first phase resides at the address 00007FF6`88F61357 (bomb+0x11357).
The first phase is the easiest one. The flow is very simple. This function doesn't even parse the input.
Core Logic
The core logic of the function is as follows:
phase_1 (our_string_1) {
if (strings_not_equal(our_string_1, "I am just a renegade hockey mom.\n") == 1)
explode_bomb()
else
return
}From this logic, we can say that our first input should be the string "I am just a renegade hockey mom." followed by the new line ("\n").
Nice, phase_1() is completed!

Phase 2
The jump to the second phase resides at the address 00007FF6`88F613CF (bomb+0x113cf).
The second phase is a bit harder than the first one, but nothing extraordinary.
Core logic
The core logic looks like this:
phase_2 (our_string_2) {
int our_six_numbers[6]
read_six_numbers(our_six_numbers, our_string_2)
if (our_six_numbers[0] != 1)
explode_bomb()
if (our_six_numbers[1] != our_six_numbers[0] * 2) // 2nd number from our input
explode_bomb()
if (our_six_numbers[2] != our_six_numbers[1] * 2) // 3rd number from our input
explode_bomb()
if (our_six_numbers[3] != our_six_numbers[2] * 2) // 4th number from our input
explode_bomb()
if (our_six_numbers[4] != our_six_numbers[3] * 2) // 5th number from our input
explode_bomb()
if (our_six_numbers[5] != our_six_numbers[4] * 2) // 6th number from our input
explode_bomb()
return
}Knowing that simple logic, we can calculate the needed input, which is 1 2 4 8 16 32, followed by the new line ("\n").
The second phase is defused. Awesome! We're flying through this thing.

Phase 3
The jump to the phase resides at the address 00007FF6`D0821410 (bomb+0x11410).
Nothing too difficult here, but the logic is less straightforward than in the second phase.
Core logic
The core logic is the following:
phase_3 (our_string_3) {
int our_two_numbers[2]
numbers_read = sscanf(our_string_3, "%d %d", our_two_numbers[0], our_two_numbers[1])
if (numbers_read < 2)
explode_bomb()
if (our_two_numbers[0] > 7)
explode_bomb()
array = [628, -588, 688, -126, 126, -126, 126, -126]
int result = 0
for (counter = our_two_numbers[0] - 1; counter < length(array), counter++) {
result += array[counter]
}
if (our_two_numbers[0] > 5)
explode_bomb()
if (our_two_numbers[1] != result)
explode_bomb()
return
}As we have this check if our_two_numbers[0] > 5, we can just delete the looser one before the loop our_two_numbers[0] > 7.
phase_3 (our_string_3) {
int our_two_numbers[2]
numbers_read = sscanf(our_string_3, "%d %d", our_two_numbers[0], our_two_numbers[1])
if (numbers_read < 2)
explode_bomb()
array = [628, -588, 688, -126, 126, -126, 126, -126]
int result = 0
for (counter = our_two_numbers[0] - 1; counter < length(array), counter++) {
result += array[counter]
}
if (our_two_numbers[0] > 5)
explode_bomb()
if (our_two_numbers[1] != result)
explode_bomb()
return
}As the first number can't be greater than 5, we can just disregard the last 2 operations as, in total, they don't change result.
Answer
I included both signed and unsigned integers as there are no signed types in assembly.

So, the answer to this stage will be such pairs of values followed by the new line ("\n"):5 -126 or 5 42949671704 03 -126 or 3 42949671702 5621 -26 or 1 42949672700 602
Voila, the third phase is defused.

Phase 4
The jump to the phase resides at the address 00007FF6`D08210AF (bomb+0x110af).
In this phase, things start to get harder. Phase 4 incorporates a recursive function.
Core logic
The core logic is as such:
phase_4 (our_string_4) {
int our_two_numbers[2]
numbers_read = sscanf(our_string_4, "%d %d", our_two_numbers[0], our_two_numbers[1])
if (numbers_read < 2)
explode_bomb()
if (our_two_numbers[0] > 0xE) // 14
explode_bomb()
result = func4 (our_two_numbers[0])
if (result != 0xA) // 10
explode_bomb()
if (our_two_numbers[1] != result)
explode_bomb()
return
}So, from the start, we have limitations that our_two_numbers[0] < 14, our_two_numbers[1] = 10, and our_two_numbers[1] = result.
func4 exploration
Now, to understand what the exact value should our first number be, it is necessary to outline the logic behind func4() recursive function:
func4 (number, parameter_1 = 0, parameter_2 = 14) {
// If the parameter_1 is not passed - parameter_1 = 0,
// and if parameter_2 is not passed - parameter_2 = 14,
// e.g. during the first call
value = parameter_2 - parameter_1
value = value - 0
value = value / 2
value = value + parameter_1
if (number < value)
return func(number, parameter_1, value - 1) + value
else if (number > value)
return func(number, value + 1, parameter_2) + value
else // number == value
return value
}Let's begin our investigation. First, we need to look at the arguments passed to the function and the expected results.
First call to func4
We pass the first number from our pair of numbers and expect the result to be 0xA (10). So, we have such equation func4(our_two_numbers[0], 0, 14) = 10. As the function should return 0xA (10), the first call should be executed along the first branch. The other two branches aren't valid for the first call because:
- The second branch implies that the
result = func(our_two_numbers[0], 8, 14) + 7and our number is greater than 7. Even in the best outcome (our_two_numbers[0] = 8),result = func(our_two_numbers[0], 8, 10) + 11 + 7, which is greater than the result that we need0xA (10), - The third branch implies that our first number and
valueare equal, so the function will return7, but we need0xA (10).
So, now we know that our_two_numbers[0] < 7.
Second call to func4
Let's explore the second call tofunc4(). We can say that the second call to our function should return 10 - 7 = 3. So func(our_two_numbers[0], 0, 6) = 3.
For the second call to return 3, it should be executed along the third branch:
- the first and second branches will return
func(our_two_numbers[0], 3, 6) + 3orfunc(our_two_numbers[0], 0, 3) + 3, which is greater than we need.
Thus, we determined that for the function to return 0xA (10), we need our first number to be 3.
Answer
Congratulations, we have defused the fourth phase with the pair 3 10 followed by the new line ("\n").

Phase 5
The jump to the fifth phase resides at the address 00007FF6`D082141F (bomb+0x1141f).
Personally, I think that the recursion function in Phase 4 was more difficult.
Core logic
The core logic of the fifth phase is represented below:
phase_5 (our_string_5) {
int our_two_numbers[2]
numbers_read = sscanf(our_string_5, "%d %d", our_two_numbers[0], our_two_numbers[1])
if (numbers_read < 2)
explode_bomb()
array = [10, 2, 14, 7, 8, 12, 15, 11, 0, 4, 1, 13, 3, 9, 6, 5]
value = 0
counter = 0
for (next_element = our_two_numbers[0]; next_element != 0xF; next_element = array[next_element]) {
value = value + array[next_element]
counter++
}
if (counter != 0xF) // 15. If the for loop didn't traverse the whole list
expolde_bomb()
if (our_two_numbers[1] != value)
expolde_bomb()
return
}As we can see, to exit the for loop, we need next_number = 15. So, basically, when we exit the loop, our values should be the following: counter = 15, next_element = 15, our_two_numbers[1] = value.
Knowing that information, we can simply traverse the loop backward:
counter = 15, next_element = 15, value = our_two_numbers[1]counter = 14, next_element = 6, value = value + 15counter = 13, next_element = 14, value = value + 6counter = 12, next_element = 2, value = value + 14counter = 11, next_element = 1, value = value + 2counter = 10, next_element = 10, value = value + 1counter = 9, next_element = 0, value = value + 10counter = 8, next_element = 8, value = value + 0counter = 7, next_element = 4, value = value + 8counter = 6, next_element = 9, value = value + 4counter = 5, next_element = 13, value = value + 9counter = 4, next_element = 11, value = value + 13counter = 3, next_element = 7, value = value + 11counter = 2, next_element = 3, value = value + 7counter = 1, next_element = 12, value = value + 3counter = 0, next_element = 5, value = 12
We know that next_element before the start of the loop is equal to our_two_numbers[0], and our_two_numbers[1] should be equal to value at the end of the loop. So, our_two_numbers[1] = 12 + 3 + 7 + 11 + 13 + 9 + 4 + 8 + 0 + 10 + 1 + 2 + 14 + 6 + 15 = 115.
Answer
The answer is 5 115.
Hurray! We found the pair of numbers that will defuse the fifth phase.

Phase 6
The jump to the sixth phase resides at the address 00007FF6`D0821136 (bomb+0x11ba6).
The core logic of Phase 6 is infinitely simpler than the actions the code does to achieve it. It was the hardest phase to analyze so far.
Core logic
The core logic of the fifth phase is represented below:
phase_6 (our_string_6) {
int our_six_numbers[6]
read_six_numbers(our_six_numbers, our_string_6)
for (counter_1 = 0; counter_1 < 5; counter_1++) {
for (counter_2 = counter_1 + 1; counter_2 < 6; counter_2++) {
// Explodes if any two elements of the array are equal (not unique)
if (our_six_numbers[counter_1] == our_six_numbers[counter_2])
explode_bomb()
}
}
array = [0x212, 0x1c2, 0x215, 0x393, 0x3a7, 0x200]
for (counter = 1; counter < 6; counter++) {
// If the elements of the array is not sorted by our numbers (indexes) in a descending order
// For example, if our first two numbers are [2, 1], the bomb will explode cause 0x1c2 <= 0x212
if (array[our_six_numbers[counter-1]-1] <= array[our_six_numbers[counter]-1])
explode_bomb()
}
return
}Answer
So, our input to defuse this function should be 5 4 3 1 6 2.

Optional: What the code does
The core logic of phase_6() looks pretty simple, right? However, it won't be that simple if we take a look at what the code does to achieve this logic, specifically, the second for loop.
Actually, before that, I should also mention that array looks differently (let's name it array_1):
| Memory address | int number | int index | int64 next_element |
|---|---|---|---|
| 00007ff7`8b8cf000 | 00000200 | 00000006 | 00000000`00000000 |
| 00007ff7`8b8cf010 | 000003a7 | 00000005 | 00007ff7`8b8cf000 |
| 00007ff7`8b8cf020 | 00000393 | 00000004 | 00007ff7`8b8cf010 |
| 00007ff7`8b8cf030 | 00000215 | 00000003 | 00007ff7`8b8cf020 |
| 00007ff7`8b8cf040 | 000001c2 | 00000002 | 00007ff7`8b8cf030 |
| 00007ff7`8b8cf050 | 00000212 | 00000001 | 00007ff7`8b8cf040 |
First of all, the code creates another array, let's say array_2 at rbp+78h. Into that array, it places Memory addresses of the array_1 elements with index that corresponds to our input numbers.
Let's say our input numbers are [3, 2, 5, 6, 1, 4], then array_2 will look like this [00007ff7`8b8cf030, 00007ff7`8b8cf040, 00007ff7`8b8cf010, 00007ff7`8b8cf000, 00007ff7`8b8cf050, 00007ff7`8b8cf020].
After that, the code changes array_1 so the next_element of the array_1 at the memory address array_2[element] points to the array_2[element+1]. It also nulls out the next_element at the address of array_2[last_element].
For example, if our array_2 looks like the one from the paragraph above, our resulting array_1 will look like this:
| Memory address | int number | int index | int64 next_element |
|---|---|---|---|
| 00007ff7`8b8cf000 | 00000200 | 00000006 | 00007ff7`8b8cf050 |
| 00007ff7`8b8cf010 | 000003a7 | 00000005 | 00007ff7`8b8cf000 |
| 00007ff7`8b8cf020 | 00000393 | 00000004 | 00000000`00000000 |
| 00007ff7`8b8cf030 | 00000215 | 00000003 | 00007ff7`8b8cf040 |
| 00007ff7`8b8cf040 | 000001c2 | 00000002 | 00007ff7`8b8cf010 |
| 00007ff7`8b8cf050 | 00000212 | 00000001 | 00007ff7`8b8cf020 |
And finally, the code checks whether our input numbers sorted array_1's numbers in descending order, i.e., if every number at next_element is less than the previous number starting from the array_2[0] address or index that is equal to our_six_numbers[0].
Getting into the secret phase
Yeah, you've read it right: there is a secret phase. How did I find out?
Let's take a look at the function that executes after each phase_*() function.
phase_defused() function explained
The jump to the function resides at the address 00007FF6`88F612A8 (bomb+0x112a8).
The core logic of the function is this:
phase_defused () {
if (num_input_strings != 6) {
return
} else {
if (sscanf(our_string_4, "%d %d %s", our_two_numbers[0], our_two_numbers[1], our_secret) != 3) {
puts("Congratulations! You've defused the bomb!.")
} else {
if (strings_not_equal(our_secret, "DrEvil") == 1) {
puts("Congratulations! You've defused the bomb!.")
} else {
puts("Curses, you've found the secret phase!.")
puts("But finding it and solving it are quite different...")
secret_phase()
puts("Congratulations! You've defused the bomb!.")
}
}
}
}Wow! We've found something interesting! Call the police!

Secret phase
The jump to the secret phase resides at the address 00007FF7`8B8C10B4 (bomb+0x110b4).
When I said that analyzing the sixth phase was hard, little did I know there was a secret phase. And, man, oh man, was it hard but also satisfying.
Core logic
Lets begin with the core logic:
secret_phase () {
our_string_secret = read_line(our_input)
our_number = atoi(our_string_secret)
if (our_number < 1) // This covers the case when atoi fails, as it returns 0 in such case
explode_bomb()
if (our_number > 0x3E9) // 1001
explode_bomb()
if (fun7(0x24, our_number) != 5) // 0x24 = 36
explode_bomb()
puts(Wow! You've defused the secret stage!.")
phase_defused()
return
}The depths of fun7
Obviously, the author of the Bomb Lab loves recursive functions, as fun7() is the second one after func4(). The jump to this function resides at 00007FF6`7D4B1028 (bomb+0x11028).
The function implements such actions:
array = [
[0x24, 1, 2],
[0x8, 3, 4],
[0x32, 5, 6],
[0x6, 7, 8],
[0x16, 9, 10],
[0x2D, 11, 12],
[0x6B, 13, 14],
[0x1, 15, 15],
[0x7, 15, 15],
[0x14, 15, 15],
[0x23, 15, 15],
[0x28, 15, 15],
[0x2F, 15, 15],
[0x63, 15, 15],
[0x3E9, 15, 15],
[0, 0, 0]
]
fun7 (parameter = array[0], our_number) {
if (parameter[0] != 0) {
if (our_number < parameter[0]) { // 1st branch
return (fun7(array[parameter[1]], our_number) * 2)
} else if (our_number > parameter[0]) { // 2nd branch
return (fun7(array[parameter[2]], our_number) * 2 + 1)
} else { // our_number == parameter[0]. 3rd branch
return 0
}
} else {
return 0xFFFFFFFF
}
}I can imagine your face after reading the pseudo code above.

Our array
It will be much easier when I explain it.
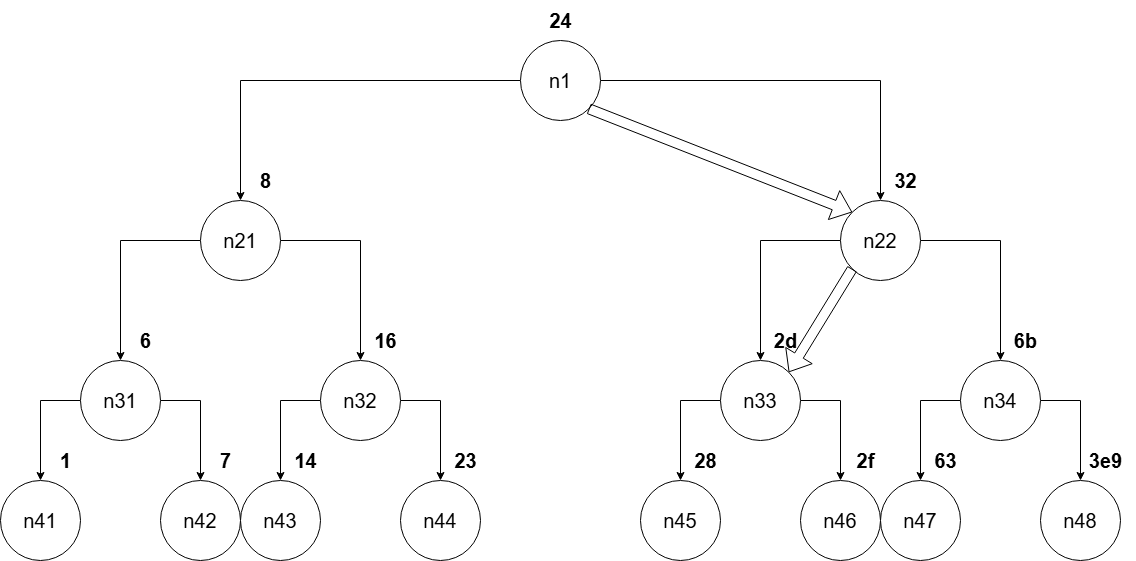
First, let's imagine such a tree, which essentially represents our array (all numbers are hex):
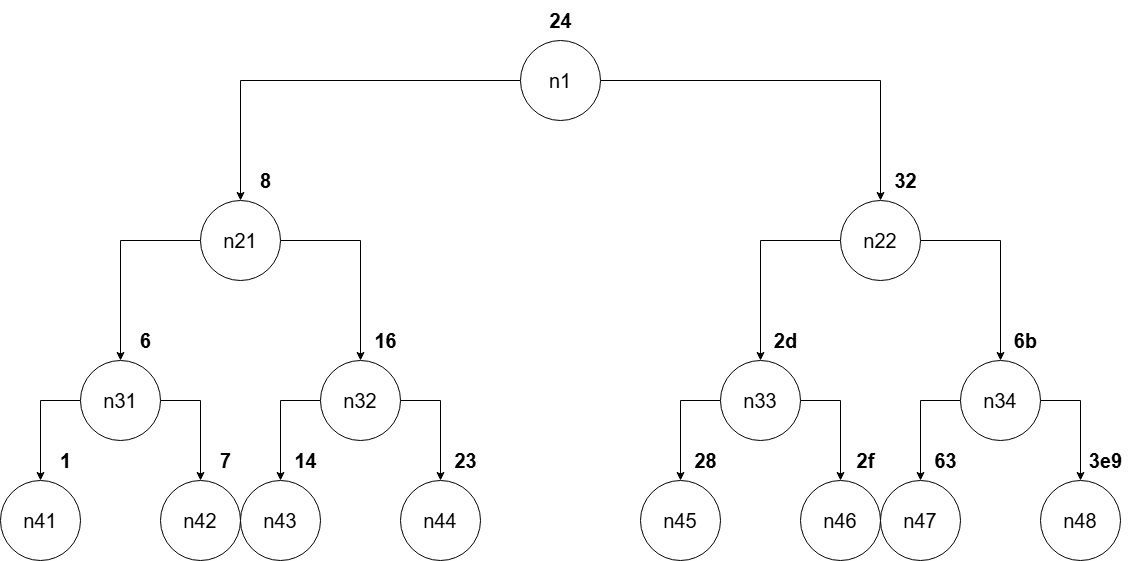
fun7 execution rules
With such representation, it is worth mentioning:
- If the call goes along the first branch, the parameter with which we execute the next call to
fun7()will be the number on the left branch of the tree, - If the call executes along the second branch,
parameterof the next call will be on the right branch of the tree, - If the function executes along the third branch, the current call is the last one, and
our_number = parameter = current array/tree leaf. - If we traverse the array/tree till the end but the last call's
our_number != parameter != current array/tree leaf, the function will return0xFFFFFFFF.
For example, if our_number = 0x25, the second call will execute with parameter = 0x32 and so on.
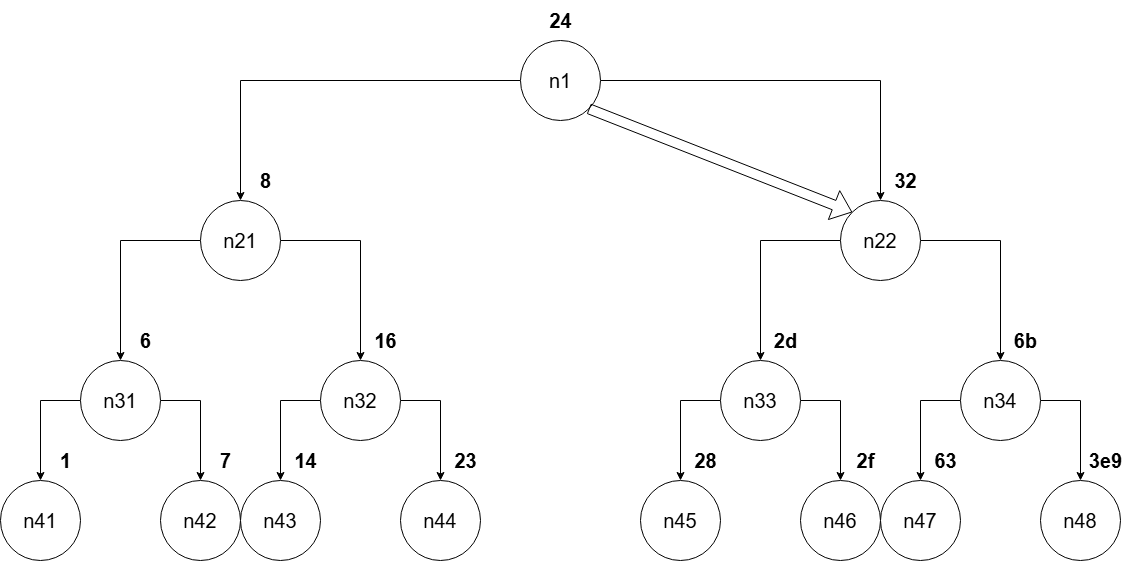
Explaining fun7 and finding the answer
So, we have our function:
fun7 (parameter = array[0], our_number) {
if (parameter[0] != 0) {
if (our_number < parameter[0]) { // 1st branch
return (fun7(array[parameter[1]], our_number) * 2)
} else if (our_number > parameter[0]) { // 2nd branch
return (fun7(array[parameter[2]], our_number) * 2 + 1)
} else { // our_number == parameter[0]. 3rd branch
return 0
}
} else {
return 0xFFFFFFFF
}
}and the array/tree:
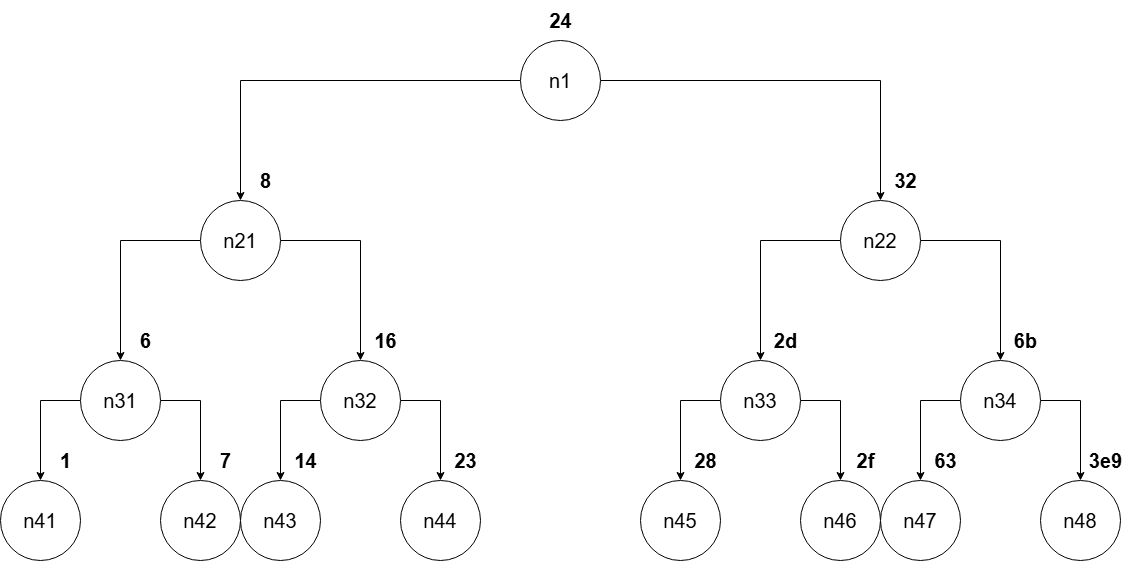
Now, let's find the answer. From the core logic of secret_phase(), we can see that we need fun7() to return 5 to defuse this phase.
First call to fun7
For fun7() to return 5, we need the first call to be executed along the second branch. Why is that?
- The first branch cannot return an odd number
- The third branch can only return 0
If the first call is executed along the second branch, the second call should return 5 = return * 2 + 1, return = (5 - 1) / 2, return = 2. The second call will be executed with parameter[0] = 0x32.
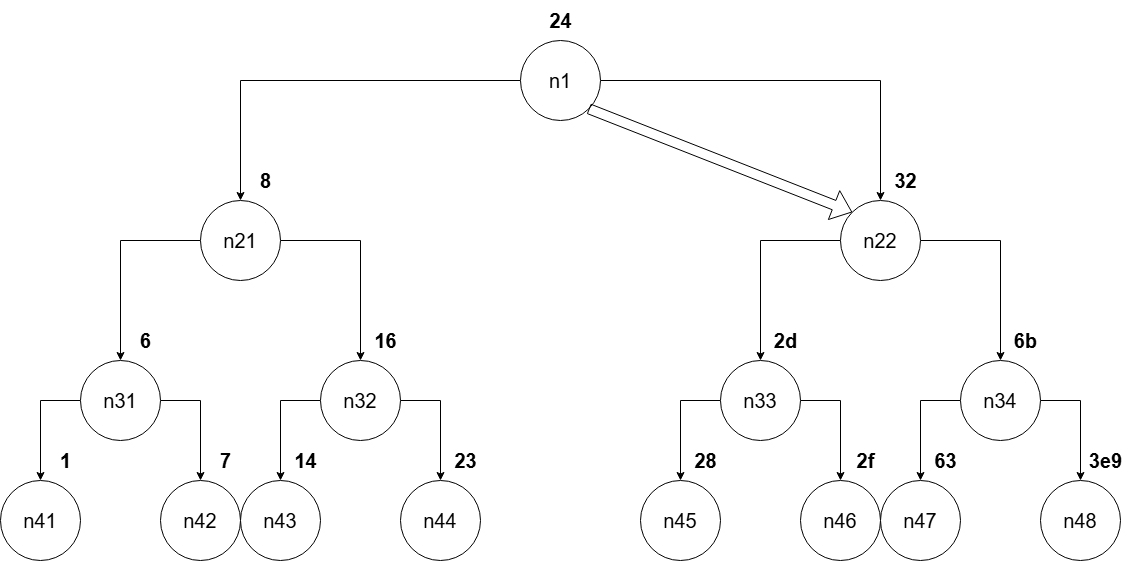
Second call to fun7
For the second call to return 2, we need it to be executed along the first branch:
- The second branch can't return even numbers
- The third branch can only return 0
If the second call is executed along the first branch, the third call shouldreturn 2 = return * 2, return = 2 / 2, return = 1. The third call will be executed with parameter[0] = 0x2d.
Third call to fun7
For the third call to return 1, we need it to be executed along the second branch:
- The first branch cannot return an odd number
- The third branch can only return 0
If the third call is executed along the first branch, the fourth call should return 1 = return * 2 + 1, return = (1 - 1) / 2, return = 0. The fourth call will be executed with parameter[0] = 0x2f.
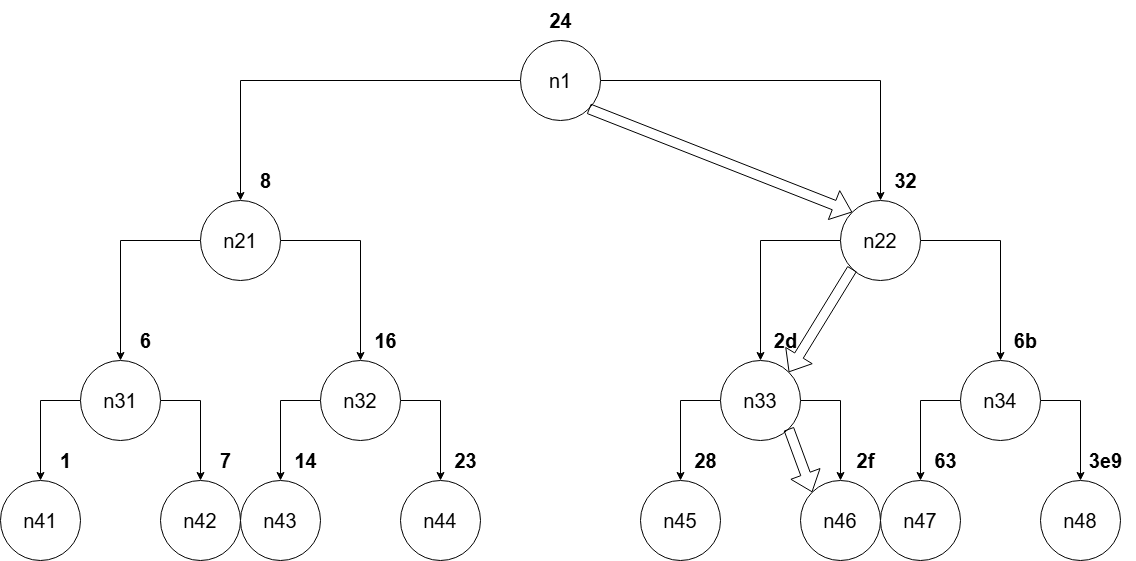
Fourth call to fun7
For the fourth call to return 0, we need it to be executed along the third branch. For it to be executed along the third branch, we need our_number == parameter[0]. parameter[0] during the fourth call is 0x2f = 47.
Answer
So, the answer to the secret phase is 47.

Answers to all phases
In the end, our answer file should look like this.
I am just a renegade hockey mom.
1 2 4 8 16 32
4 0
3 10 DrEvil
5 115
5 4 3 1 6 2
47Afterword
Whew, what a journey that was. I had a wonderful time solving the Bomb Lab from Xeno's course Architecture 1001: x86-64 Assembly. Thank you, Xeno, for sharing your knowledge and creating such interesting material.
I'm very proud I solved it without external help and symbols. I did solve it with symbols the first time, but I brute-forced some phases' solutions, avoiding fully analyzing the code. But I'm glad I decided to write this post as in the process of making it, I discovered some details I wouldn't find otherwise.
Finally, I would like to thank everyone who is reading this post. I hope it helps you or entertains you. See you in the future!

Time spent on preparing and publishing this post: 21h 36m.